|
Lycia Home |
Lycis Cnidos |
Eudoxus_Home |
Algebra |
constellations |

Eudoxus of Cnidus (410 or 408 BC 355 or 347 BC) was a Greek astronomer, mathematician, physician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy. Theodosius of Bithynia's Sphaerics may be based on a work of Eudoxus.
Eudoxus was the son of Aeschines of Cnidus, located in Asia Minor. Eudoxus first travelled to Tarentum to study with Archytas, from whom he learned mathematics. While in Italy, Eudoxus visited Sicily, where he studied medicine with Philiston.
Around 387 BC, at the age of 23, he traveled with the physician Theomedon to Athens to study with the followers of Socrates. He eventually became the pupil of Plato, with whom he studied for several months, but due to a disagreement they had a falling out. Eudoxus was quite poor and could only afford an apartment at the Piraeus. To attend Plato's lectures, he walked the seven miles each direction, each day. Due to his poverty, his friends raised funds sufficient to send him to Heliopolis, Egypt to pursue his study of astronomy and mathematics. He lived there 16 months. From Egypt, he then traveled north to Cyzicus, located on the south shore of the Sea of Marmara, and the Propontis. He traveled south to the court of Maussolus. During his travels he gathered many students of his own.
Around 368 BC, he returned to Athens with his students. Eudoxus eventually returned to his native Cnidus, where he served in the city assembly. While in Cnidus, he built an observatory and continued writing and lecturing on theology, astronomy and meteorology. He had one son, Aristagoras, and three daughters, Actis, Philtis and Delphis.
In mathematical astronomy his fame is due to the introduction of the astronomical globe, and his early contributions to understanding the movement of the planets.
His work on proportions shows tremendous insight into numbers; it allows rigorous treatment of continuous quantities and not just whole numbers or even rational numbers. When it was revived by Tartaglia and others in the 1500s, it became the basis for quantitative work in science for a century, until it was replaced by the algebraic methods of Descartes.
Eudoxus rigorously developed Antiphon's method of exhaustion, which was used in a masterly way by Archimedes. The work of Eudoxus and Archimedes as precursors of calculus was only exceeded in mathematical sophistication and rigour by Indian Mathematician Bhaskara and later by Newton.
In ancient Greece, astronomy was a branch of mathematics; astronomers sought to create geometrical models that could imitate the appearances of celestial motions. Identifying the astronomical work of Eudoxus as a separate category is therefore a modern convenience. Some of Eudoxus' astronomical texts whose names have survived include:
- Disappearances of the Sun, possibly on eclipses
- Oktaeteris, on an eight-year lunisolar cycle of the calendar
- Phaenomena and Entropon, on spherical astronomy, probably based on observations made by Eudoxus in Egypt and Cnidus
- On Speeds, on planetary motions
We are fairly well informed about the contents of Phaenomena, for Eudoxus' prose text was the basis for a poem of the same name by Aratus. Hipparchus quoted from the text of Eudoxus in his commentary on Aratus.





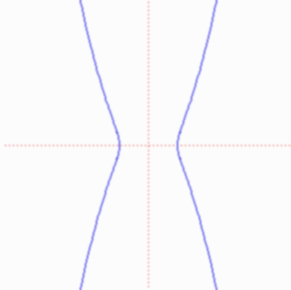
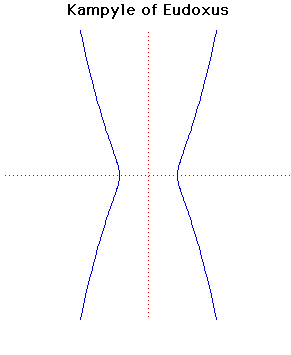
 ))
))

 wikimedia curves -
wikimedia curves - 


![[Graphics:Images/index_gr_139.gif]](index_gr_139.gif)
![[Graphics:Images/index_gr_142.gif]](index_gr_142.gif)
![[Graphics:Images/index_gr_143.gif]](index_gr_143.gif)
![[Graphics:Images/index_gr_144.gif]](index_gr_144.gif)





