|
|
|
Eudoxus
Nomenclature
|
|
eudoxus The Cambridge History of Hellenistic PhilosophyBy Keimpe Algra |
The Secret Life of an Alchemist: Francis Bacon's Real Philosophy of Nature by John Henry University of Edinburgh Science Studies Unit .....................
This diagram shows how the Eudoxan combination of spheres rotating within spheres (with different axes of rotation, but always with the same centre of rotation) can give rise to the loop-the-loop motion characteristic of planetary retrograde motion.  Although the theory of homocentric spheres had never been taken up by astronomers, it attracted renewed attention in the Renaissance as a result of the crisis facing Ptolemaic astronomy. In particular, the system developed by the Andalusian philosopher Al-Bitruji, known to the Latins as Alpetragius, looked promising. In particular it seemed to have one advantage over the Ptolemaic system. ......... |
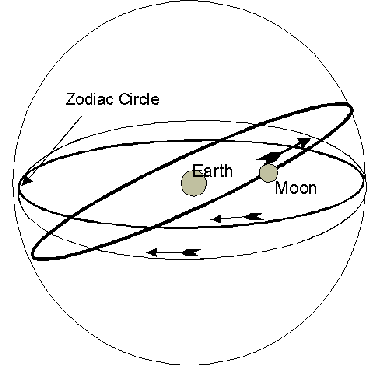
Eudoxan planetary modelsA general idea of the content of On Speeds can be gleaned from Aristotle's Metaphysics XII, 8, and a commentary by Simplicius of Cilicia (6th century CE) on De caelo, another work by Aristotle. According to a story reported by Simplicius, Plato posed a question for Greek astronomers: "By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for?" (quoted in Lloyd 1970, p. 84). Plato proposed that the seemingly chaotic wandering motions of the planets could be explained by combinations of uniform circular motions centered on a spherical Earth, apparently a novel idea in the 4th century. In most modern reconstructions of the Eudoxan model, the Moon is assigned three spheres:
The Sun is also assigned three spheres. The second completes its motion in a year instead of a month. The inclusion of a third sphere implies that Eudoxus mistakenly believed that the Sun had motion in latitude. The five visible planets (Venus, Mercury, Mars, Jupiter, and Saturn) are assigned four spheres each:
Importance of Eudoxan systemCallippus, a Greek astronomer of the 4th century, added seven spheres to Eudoxus' original 27 (in addition to the planetary spheres, Eudoxus included a sphere for the fixed stars). Aristotle described both systems, but insisted on adding "unrolling" spheres between each set of spheres to cancel the motions of the outer set. Aristotle was concerned about the physical nature of the system; without unrollers, the outer motions would be transferred to the inner planets. A major flaw in the Eudoxan system is its inability to explain changes in the brightness of planets as seen from Earth. Because the spheres are concentric, planets will always remain at the same distance from Earth. This problem was pointed out in Antiquity by Autolycus of Pitane. Astronomers responded by introducing the deferent and epicycle, which caused a planet to vary its distance. However, Eudoxus' importance to Greek astronomy is considerable, as he was the first to attempt a mathematical explanation of the planets.
|
Eudoxus of CnidusFrom WikipediaNot to be confused with Eudoxus of Cyzicus. Eudoxus of Cnidus (Greek Εὔδοξος ὁ Κνίδιος) (410 or 408 BC – 355 or 347 BC) was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy. Theodosius of Bithynia's Sphaerics may be based on a work of Eudoxus.
LifeEudoxus was the son of Aeschines of Cnidus, located in Asia Minor. Eudoxus first travelled to Tarentum to study with Archytas, from whom he learned mathematics. While in Italy, Eudoxus visited Sicily, where he studied medicine with Philiston. Around 387 BC, at the age of 23, he traveled with the physician Theomedon, who had been his erastes,[1] to Athens to study with the followers of Socrates. He eventually became the pupil of Plato, with whom he studied for several months, but due to a disagreement they had a falling out. Eudoxus was quite poor and could only afford an apartment at the Piraeus. To attend Plato's lectures, he walked the seven miles each direction, each day. Due to his poverty, his friends raised funds sufficient to send him to Heliopolis, Egypt to pursue his study of astronomy and mathematics. He lived there 16 months. From Egypt, he then traveled north to Cyzicus, located on the south shore of the Sea of Marmara, and the Propontis. He traveled south to the court of Mausolus. During his travels he gathered many students of his own. Around 368 BC, he returned to Athens with his students. Eudoxus eventually returned to his native Cnidus, where he served in the city assembly. While in Cnidus, he built an observatory and continued writing and lecturing on theology, astronomy and meteorology. He had one son, Aristagoras, and three daughters, Actis, Philtis and Delphis. In mathematical astronomy his fame is due to the introduction of the astronomical globe, and his early contributions to understanding the movement of the planets. His work on proportions shows tremendous insight into numbers; it allows rigorous treatment of continuous quantities and not just whole numbers or even rational numbers. When it was revived by Tartaglia and others in the 16th century, it became the basis for quantitative work in science for a century, until it was replaced by the algebraic methods of Descartes. Eudoxus rigorously developed Antiphon's method of exhaustion, which was used in a masterly way by Archimedes. The work of Eudoxus and Archimedes as precursors of calculus was exceeded in mathematical sophistication and rigour only by Indian Mathematician Bhaskara II (1114-1185 C.E.) and by Isaac Newton (1642-1727). An algebraic curve (the Kampyle of Eudoxus) is named after him
Also, craters on Mars and the Moon are named in his honor. MathematicsThe Pythagoreans had discovered that the diagonal of a square does not have a common unit of measurement with the sides of the square; this is the famous discovery that the square root of 2 cannot be expressed as the ratio of two integers. This discovery had heralded the existence of incommensurable quantities beyond the integers and rational fractions, but at the same time it threw into question the idea of measurement and calculations in geometry as a whole. For example, Euclid provides an elaborate proof of the Pythagorean theorem, by using addition of areas instead of the much simpler proof from similar triangles, which relies on ratios of line segments. Ancient Greek mathematicians calculated not with quantities and equations as we do today, but instead they used proportionalities to express the relationship between quantities. Thus the ratio of two similar quantities was not just a numerical value, as we think of it today; the ratio of two similar quantities was a primitive relationship between them. Eudoxus was able to restore confidence in the use of proportionalities by providing an astounding definition for the meaning of the equality between two ratios. This definition of proportion forms the subject of Euclid's Book V. In Definition 5 of Euclid's Book V we read: Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth when, if any equimultiples whatever be taken of the first and third, and any equimultiples whatever of the second and fourth, the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively taken in corresponding order. Let us clarify it by using modern-day notation. If we take four quantities: a, b, c, and d, then the first and second have a ratio a/b; similarly the third and fourth have a ratio c/d. Now to say that a/b = c/d we do the following: For any two arbitrary integers, m and n, form the equimultiples m*a and m*c of the first and third; like-wise form the equimultiples n*b and n*d of the second and fourth. Now, if it happens that m*a > n*b, then we must also have m*c > n*d. If it happens that m*a = n*b, then we must also have m*c = n*d. Finally, if it happens that m*a < n*b, then we must also have m*c < n*d. Notice that the definition depends on comparing the similar quantities m*a and n*b, and the similar quantities m*c and n*d, and does not depend on the existence of a common unit of measuring these quantities. The complexity of the definition reflects the deep conceptual and methodological innovation involved. It brings to mind the famous Fifth postulate of Euclid concerning parallels, which is more extensive and complicated in its wording than the other postulates. The Eudoxian definition of proportionality uses the quantifier, "for every ..." to harness the infinite and the infinitesimal, just as the modern epsilon-delta definitions of limit and continuity. AstronomyIn ancient Greece, astronomy was a branch of mathematics; astronomers sought to create geometrical models that could imitate the appearances of celestial motions. Identifying the astronomical work of Eudoxus as a separate category is therefore a modern convenience. Some of Eudoxus' astronomical texts whose names have survived include:
We are fairly well informed about the contents of Phaenomena, for Eudoxus' prose text was the basis for a poem of the same name by Aratus. Hipparchus quoted from the text of Eudoxus in his commentary on Aratus. Eudoxan planetary modelsA general idea of the content of On Speeds can be gleaned from Aristotle's Metaphysics XII, 8, and a commentary by Simplicius of Cilicia (6th century CE) on De caelo, another work by Aristotle. According to a story reported by Simplicius, Plato posed a question for Greek astronomers: "By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for?" (quoted in Lloyd 1970, p. 84). Plato proposed that the seemingly chaotic wandering motions of the planets could be explained by combinations of uniform circular motions centered on a spherical Earth, apparently a novel idea in the 4th century. In most modern reconstructions of the Eudoxan model, the Moon is assigned three spheres:
The Sun is also assigned three spheres. The second completes its motion in a year instead of a month. The inclusion of a third sphere implies that Eudoxus mistakenly believed that the Sun had motion in latitude. The five visible planets (Venus, Mercury, Mars, Jupiter, and Saturn) are assigned four spheres each:
Importance of Eudoxan systemCallippus, a Greek astronomer of the 4th century, added seven spheres to Eudoxus' original 27 (in addition to the planetary spheres, Eudoxus included a sphere for the fixed stars). Aristotle described both systems, but insisted on adding "unrolling" spheres between each set of spheres to cancel the motions of the outer set. Aristotle was concerned about the physical nature of the system; without unrollers, the outer motions would be transferred to the inner planets. A major flaw in the Eudoxan system is its inability to explain changes in the brightness of planets as seen from Earth. Because the spheres are concentric, planets will always remain at the same distance from Earth. This problem was pointed out in Antiquity by Autolycus of Pitane. Astronomers responded by introducing the deferent and epicycle, which caused a planet to vary its distance. However, Eudoxus' importance to Greek astronomy is considerable, as he was the first to attempt a mathematical explanation of the planets.
|
|
Eudoxus of Cnidus Eudoxus (c. 400 B.C.) is the greatest of the ancient mathematicians, surpassed only by Archimedes -- but later. Biographical highlights:
Eudoxus was the most reknown astronomer and mathematician of his day. In astronomy devised an ingenious planetary system based on spheres.
Consider the moon.
Homocentric spheres for the moon
~~~~~~~~~~~~~~~~~~~~~~~~ Eudoxus 's contributions to mathematics include:
There is little question that Eudoxus added to the body of geometric knowledge. Details are scant, but probably his main contributions can be found in Euclid, Books V, VI, and XII. The Theory of Proportion of Eudoxus is found as Definition 5 of Euclid, Book V. Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when, if any equimultiples whatever be taken of the first and third, and any equimultiples whatever of the second and fourth, the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively tken in corresponding order. In modern terms: a/b=c/d if and only if, for all integers m and n , whenever ma<nb then mc<nd, and so on for > and =. This is tantamount to an infinite process. But it was needed to deal with incommensurables. The Method of Exhaustion unquestionably helped resolve number of loose ends then extant. It contained as Proposition 1 of Book X.
Two unequal magnitudes being set out, if from the greater there is subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process be repeated continually, there will be left some magnitude which will be less than the lesser magnitude set out.
Let How does this differ from our limit concept today? With this result, Eudoxus was able to establish following: Proposition 2. (Book XII) Circles are to one another as the squares on the diameters.This was proved on the basis of the previous proposition. Proposition 1. (Book XII) Similar polygons inscribed in circles are to one another as the squares on the diameters. To prove the Proposition 2, polygonal figures, of indefinitely increasing numbers of sides, are both inscribed and circumscribed in the circle. Assuming Proposition 2 does not hold will lead to the contratiction that the result must be false for the polygons also. Proof of Proposition 2. Let a and A, d and D be the repectively diameters of the circles. Suppose that
Then there is an a'<a so that
Set
By the method of exhaustion it follows that for large enough n which implies that
We know that
Thus, since To complete the proof, it must now be shown that
is also impossible. This is a double reductio ad absurdum argument, a requirement of this method. Eudoxus also demonstrated that the ratios of the volumes of two spheres is as the cube On pyramids Eudoxus proved Proposition 5. (Book XII) Pyramids which are of the same height and have triangular bases are to each other as their bases. Other propositions are more famous Proposition. The volume of every pyramid is one third of the prism of on the same base and with the same height. Proposition. The volume of every cone is one third of the cylinder on the same base and with the same height. Curiously, the proof is by the method of slabs, familiar to all freshmen. http://www.math.tamu.edu/~dallen/history/eudoxus/eudoxus.html |